The examples in this article are for a Renaissance lute in g’.
All through music history several systems of tuning were used. Some of these tunings, also known as temperaments, sound very well on renaissance lutes. Mean-tone temperament, in which you have pure thirds, is especially good. It is not so difficult to tune your lute in mean-tone temperament, and the result is absolutely worthwhile. In this article I will explain about mean-tone temperament and show you how to reposition your frets and tune your strings for it. Finally, I will explain how to put your frets back into their positions for equal temperament.
In this article I will use cents. One cent is defined as the 100th part of the difference in pitch between two notes half a tone apart in equal temperament. It is easier to use cents then frequencies in Hertz when writing about temperaments.
Pure tuning is impossible
As Pythagoras already knew in the 5th century B.C., pure intervals are natural harmonics and therefore simple relations between frequency ratios:
1 : 2 octave (1200 cents)
2 : 3 fifth (701.96 cents)
3 : 4 fourth (498.04 cents)
4 : 5 major third (386.31 cents)
5 : 6 minor third (315.64 cents)
If you take a c, and add 12 pure fifths to it, you will get a b-sharp6. The frequency ratio between c and b-sharp6 is 12 times 2 : 3 equals 4096 : 531441.
If you take the same c, and add 7 pure octaves, you will get a c7. The frequency ratio between c and c7 is 7 times 1 : 2 equals 4096 : 524288.
The pitches b-sharp6 and c7 are enharmonically the same; they share the same key on the piano and the same fret on the lute. However, the result of calculating them via pure fifths or via pure octaves is not the same. The difference is called the Pythagorean comma. It is exactly 23.46 cents.
To make a workable system of tuning for the lute, after all, you can have only one fret for a b-sharp and a c, this Pythagorean comma has to be gotten rid of. To think about this, it helps to imagine a circle of fifths:
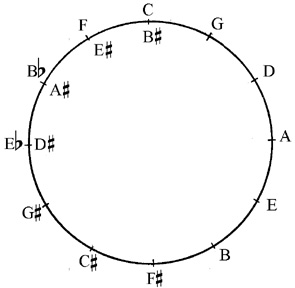
Equal temperament
The easiest way of spreading out the Pythagorean comma is to divide it equally over all 12 fifths. This system of tuning is called equal temperament and modern instruments like guitars and pianos are tuned in equal temperament. In equal temperament all fifths are 23.46 divided by 12, equals about 2 cents, too small (700 cents in stead of 702 cents). This is acceptable for our ears. The major thirds, however, are much too big: 400 cents instead of 386 cents. This is not very beautiful. If you play a harmonic around the fourth fret, you will hear a pure major third, try it on the fourth string, then you will hear an a. Compare this to the equal third, the normal a on the second fret on the first string, and you will hear the difference. Historical evidence suggests equal temperament was used for lutes from about 1550 onward, though Vincenzo Galilei still fulminates against the use of so called ‘tastini’ (little frets) in his Fronimo printed in 1568 and reprinted in 1584. He explains that lute players of his time add these to ‘remove some of the sharpness from the thirds and major tenths’. To me, that reads like an advertisement in favour of mean-tone temperament; who wouldn’t want the sharpness from his thirds removed? Early 17th century Italian music with wind instruments sounds best in mean-tone temperament. Many organs are still tuned in mean-tone temperament up to the present day.
Mean-tone temperament
If we add up four pure fifths, e.g. c – e2, the ratio between the c and the e2 is 16 : 81, the third c2 – e2 is 64 : 81. A pure major third, however, is 4 : 5. The difference between these two thirds is 80 : 81, or 21.50 cents. It is called the syntonic comma. To make a temperament in which major thirds are pure, this syntonic comma has to be gotten rid of.
Mean-tone temperament does just that: it makes 11 fifths each one quarter syntonic comma too small. The remaining fifth will be much too big. The 11 fifths are audibly too small, but still usable. The 12th fifth, however, is unusable and is called the wolf. It is sometimes used to express very harsh words in the text. Usually the wolf is between the g-sharp and the e-flat, or between the d-sharp and the b-flat, depending on which note is needed in the music: the d-sharp or the e-flat. In mean-tone temperament, all thirds are pure, which gives a wonderfully warm, sonorous sound when playing chords. A lute tuned in mean-tone temperament sounds a lot better. Other systems of mean-tone temperament do not tune the 11 fifths a quarter comma too small, but for example one sixth comma (Silbermann) or two seventh (Zarlino 1558). If you have a programmable tuning machine (like the Korg MT-1200 or the Sonic Research ST-122) you can enter the following cents deviations from equal temperament for each note:
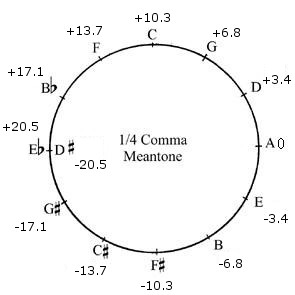
Repositioning of frets
But you don’t need a tuning machine to tune your lute in mean-tone temperament. First, take a piece of paper and place it on top of the fingerboard of the lute, one end touching the nut. Now mark the current fret positions on the paper. This way you can put your frets back in their original position later.
Now that we know how many cents higher or lower than equal temperament a note has to be in mean-tone temperament, we can calculate fret positions. Because mean-tone temperament is a temperament with equal fifths, the fret positions on different strings are the same. Here is a table with the deviations from equal temperament of each fret, incorporating the deviations from equal temperament of the open strings:
| open string | 1st fret | 2nd fret | 3rd fret | 4th fret | 5th fret | 6th fret | 7th fret | 8th fret |
| G + 6.8 | G# – 23.9 | A – 6.8 | Bb + 10.3 | B – 13.6 | C + 3.5 | C# – 20.5 | D – 3.4 | Eb + 13.7 |
| D + 3.4 | Eb + 17.1 | E – 6.8 | F + 10.3 | F# – 13.7 | G + 3.4 | G# – 20.5 | A – 3.4 | Bb + 13.7 |
| A + 0 | Bb + 17.1 | B – 6.8 | C + 10.3 | C# – 13.7 | D + 3.4 | Eb + 20.5 | E – 3.4 | F + 13.7 |
| F + 13.7 | F# – 24 | G – 6.9 | G# – 30.8 | A – 13.7 | Bb + 3.4 | B – 20.5 | C – 3.4 | C# – 27.4 |
| C + 10.3 | C# – 24 | D – 6.9 | Eb + 10.2 | E – 13.7 | F + 3.4 | F# – 20.6 | G – 3.5 | G# – 27.4 |
| G + 6.8 | G# – 23.9 | A – 6.8 | Bb + 10.3 | B – 13.6 | C + 3.5 | C# – 20.5 | D – 3.4 | Eb + 13.7 |
This results in the following list of numbers, with which you will have to multiply the string length of your lute to get the new fret positions:
| b | c | d | e | f | g | h | i |
| 0.043 0.065 |
0.106 | 0.164 | 0.200 | 0.252 | 0.284 | 0.331 | 0.360 0.375 |
For a lute with a string length of 59 cm this would result in the following fret positions in cm:
| b | c | d | e | f | g | h | i |
| 2.5 3.9 |
6.2 | 9.7 | 11.8 | 14.9 | 16.8 | 19.6 | 21.1 22.1 |
You can mark these fret positions on a similar piece of paper again.
For fret b (first) and i (eighth) we come up with two fret positions: one for notes that are higher than in equal temperament and one for notes that are lower than in equal temperament. On the first fret the higher notes are the b-flat and e-flat on the second and third string. The lower notes on the first fret are the g-sharp on string one and six, the f-sharp on the fourth string and the c-sharp on the fifth string. Some 16th century lute music takes this into account: it will use either notes for a high first fret, or for a low first fret. Notes from both groups will not occur in one piece, so you can reposition the first fret according to the piece you are playing. But if you want to use notes from both these two groups in one piece, you have to find a solution. One solution is to put the first fret obliquely: low for the lower strings, high for the higher strings. This way we can play the notes on string five and six more or less in tune, and hopefully those on string two and three as well. We cannot use the first fret on the first string, however, so this is not an ideal solution. A better plan is to put the fret in the low position and to glue a little extra fret (called tastini, Italian for ‘little frets’) in the higher position for only the second and third string. You can use a small bit of fret or matchstick and some tape. A historic solution might be to use a double first fret, like on viola da gambas, and split the fret to cover both positions. I have not tried this. Another solution is to make two frets, the lower one of thin carbon or nylon with little bits of electricity insulation cable around it. The little bits of insulation cable can be placed under the strings that need it. It takes some experimenting with thickness of material to get tastini that do not buzz, but this way you can still adjust the position of the tastini, choose which strings you want them under, and finally, push the whole fret against its neighbour when you do not want to play in mean-tone temperament any more. A friend of mine uses little custom made ebony wedges.
The i-fret (eighth) is usually no problem, you can place it in either the low or the high position, depending on the piece you play. Just try and listen.
Tuning
Now you only have the fret positions for mean-tone temperament. Next you will have to tune the open strings of the lute, too. This is simple:
* 1. Tune the third string, a, on a tuning fork or tuning machine.
* 2. Tune a pure major third downward, a-f, between the third and fourth strings. You can use the new fourth fret position, or use the harmonic above the fourth fret of the fourth string to get a pure third.
* 3. Tune the second string, d, by tuning its third fret, f, in a pure octave with the open fourth string.
* 4. Tune the fifth string, c, by tuning the open string in a pure octave with the third fret on the third string.
* 5. Tune the first string, g, by tuning the second fret, a, in a pure octave with the open third string.
* 6. Tune the sixth string, g, by tuning a pure double octave with the first string.
You are now ready to play in mean-tone temperament. You will notice that most chords sound very warm. Maybe some frets will need a little adjustment. Some notes are not usable, try the third fret on the fourth string in an E-major chord (example 1): horrible!

Or try E-major with a g-sharp on the first fret of the first string (example 2). Now try f-minor with an a-flat on the first fret of the first string (example 3).
Depending on you having made a low first fret (g-sharp) or a high first fret (a-flat), one chord will sound good, the other bad.
One sixth comma mean-tone temperament
Because many lute players prefer one sixth comma mean-tone for 16th and early 17th century repertoire, as it is not so extreme as one quarter comma or ‘true’ mean-tone temperament, I will give cents deviations from equal temperament for each note for the programmable tuning machines.
This temperament is often called Silbermann temperament, but it is not, as Silbermann used the pythagorean comma for his calculations, resulting in a fifth of 698.045 cents, as opposed to the the fifth of 698,375 cents in one sixth syntonic comma mean-tone temperament as described here.
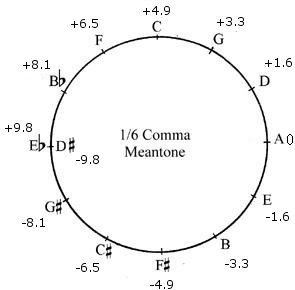
Here is the table with fret displacement compared to equal temperament, expressed in cents:
| open string | 1st fret | 2nd fret | 3rd fret | 4th fret | 5th fret | 6th fret | 7th fret | 8th fret |
| G + 3.3 | G# – 11.4 | A – 3.3 | Bb + 4.8 | B – 6.6 | C + 1.6 | C# – 9.8 | D – 1.7 | Eb + 6.5 |
| D + 1.6 | Eb + 8.2 | E – 3.2 | F + 4.9 | F# – 6.5 | G + 1.7 | G# – 9.7 | A – 1.6 | Bb + 6.5 |
| A + 0 | Bb + 8.1 | B – 3.3 | C + 4.9 | C# – 6.5 | D + 1.6 | Eb + 9.8 | E – 1.6 | F + 6.5 |
| F + 6.5 | F# – 11.4 | G – 3.2 | G# – 14.6 | A – 6.5 | Bb + 1.6 | B – 9.8 | C – 1.6 | C# – 13 |
| C + 4.9 | C# – 11.4 | D – 3.3 | Eb + 4.9 | E – 6.5 | F + 1.6 | F# – 9.8 | G – 1.6 | G# – 13 |
| G + 3.3 | G# – 11.4 | A – 3.3 | Bb + 4.8 | B – 6.6 | C + 1.6 | C# – 9.8 | D – 1.7 | Eb + 6.5 |
And here are the numbers by which you have to multiply your string length to get fret positions for one sixth syntonic comma mean-tone temperament:
| b | c | d | e | f | g | h | i |
| 0.050 0.061 |
0.107 | 0.161 | 0.203 | 0.252 | 0.289 | 0.332 | 0.366 0.372 |
For a lute with a string length of 59 cm this would result in the following fret positions in cm:
| b | c | d | e | f | g | h | i |
| 2.9 3.6 |
6.3 | 9.5 | 12.0 | 14.8 | 17.0 | 19.6 | 21.6 22.0 |
Here you can see the difference between the two frets in the first position, the b-fret, and the eighth position, the i-fret, are not so great any more.

And this is what it looks like on my 59cm 8-course lute. Notice the extra first fret for courses four to seven, and the compromise tastini for g-sharp/a-flat in the third position on the fourth course. I cannot play a g-sharp on the first fret of the first course in this configuration, so I must be carefull with E-major chords.
Ross W. Duffin argues a strong case in favour of 1/6 syntonic comma mean-tone temperament for baroque ensemble playing in his articles Why I hate Valotti (or was it Young?) and Baroque Ensemble Tuning in Extended 1/6 Syntonic Comma mean-tone.
Silbermann
Mainly because I have to play in Silbermann temperament myself quite often, and because there is some confusion with 1/6 comma mean-tone temperament, I have included the calculations for Silbermann temperament. But the difference between the two temperaments is very small.
Silbermann temperament, or Silbermann 1/6 comma temperament – there is considerable confusion over the names of the various temperaments associated with him – is one sixth pythagorean comma mean-tone temperament, as opposed to the one sixth syntonic comma mean-tone temperament described above. The Pythagorean comma is 23.46 cents, a little more than the Syntonic comma of 21.50 cents. One sixth Pythagorean comma is 3.91 cents. All pure fifths of 701.96 cents are tuned this 3.96 cents too small, resulting in fifths of 698.05 cents. That is but a little smaller than the fifth of 698.38 cents in one sixth syntonic comma mean-tone temperament described above. A fifth of 698.05 cents is 1.95 cents smaller than an equal temperament fifth of 700 cents.
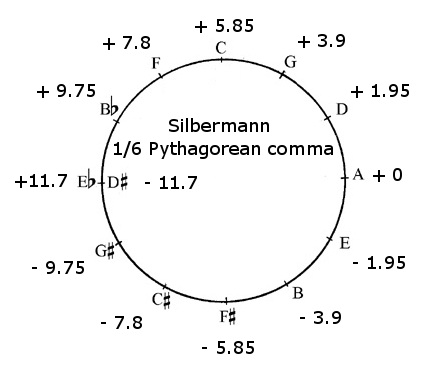
Here is the table with fret displacement compared to equal temperament, expressed in cents:
| open string | 1st fret | 2nd fret | 3rd fret | 4th fret | 5th fret | 6th fret | 7th fret | 8th fret |
| G + 3.9 | G# – 13.7 | A – 3.9 | Bb + 5.9 | B – 7.8 | C + 2.0 | C# – 11.7 | D – 2.0 | Eb + 7.8 |
| D + 2.0 | Eb + 9.8 | E – 3.9 | F + 5.9 | F# – 7.8 | G + 2.0 | G# – 11.7 | A – 2.0 | Bb + 7.8 |
| A + 0 | Bb + 9.8 | B – 3.9 | C + 5.9 | C# – 7.8 | D + 2.0 | Eb + 11.7 | E – 2.0 | F + 7.8 |
| F + 7.8 | F# – 13.7 | G – 3.9 | G# – 17.6 | A – 7.8 | Bb + 2.0 | B – 11.7 | C – 2.0 | C# – 15.6 |
| C + 5.9 | C# – 13.7 | D – 3.9 | Eb + 5.9 | E – 7.8 | F + 2.0 | F# – 11.7 | G – 2.0 | G# – 15.7 |
| G + 3.9 | G# – 13.7 | A – 3.9 | Bb + 5.9 | B – 7.8 | C + 2.0 | C# – 11.7 | D – 2.0 | Eb + 7.8 |
And here are the numbers by which you have to multiply your string length to get fret positions for one Silbermann temperament:
| b | c | d | e | f | g | h | i |
| 0.049 0.061 |
0.107 | 0.162 | 0.203 | 0.252 | 0.289 | 0.332 | 0.364 0.373 |
For a lute with a string length of 59 cm this would result in the following fret positions in cm:
| b | c | d | e | f | g | h | i |
| 2.9 3.6 |
6.3 | 9.5 | 12.0 | 14.9 | 17.0 | 19.6 | 21.5 22.0 |
As you can see, in the final result for a 59cm lute, there is virtually no difference with 1/6 syntonic comma mean-tone.
Back to equal temperament
To put your frets back into their equal temperament positions, you can either use the piece of paper on which you marked them, or calculate their exact positions by multiplying the string length of your lute with the following numbers:
| b | c | d | e | f | g | h | i |
| 0.056 | 0.109 | 0.159 | 0.206 | 0.251 | 0.293 | 0.333 | 0.370 |
Again, for a lute with a string length of 59 cm this will result in the following fret positions in cm:
| b | c | d | e | f | g | h | i |
| 3.3 | 6.4 | 9.4 | 12.2 | 14.8 | 17.3 | 19.6 | 21.8 |
Do not forget to tune the open strings back as well.
A good book for further reading is Mark Lindley’s Lutes, Viols and Temperaments (Cambridge University Press, 1984).
David van Ooijen 8/2001
This article first appeared in Nostalgia, the news letter of the Lute & Early Guitar Society of Japan.