The examples in this article are for a renaissance lute in g’.
In Pythagorean temperament, fifths are pure. A consequence of pure fifths in a temperamant for fretted instruments is that major thirds are much too wide, and minor thirds much too narrow. That makes Pythagorean temperament suitable for music in which the fifth is an important consonant and in which the third is not much used in triads. This is true of part of the medieval repertoire, hence many musicians prefer to play this music in Pythagorean temperament.
In this article I will explain about Pythagorean temperament and show you how to reposition your frets and tune your courses. Finally, I will explain how to put your frets back into their positions for equal temperament.
In this article I will use cents. One cent is defined as the 100th part of the difference in pitch between two notes half a tone apart in equal temperament. It is easier to use cents then frequencies in Hertz when writing about temperaments.
Pythagorean temperament
As Pythagoras already knew in the 5th century B.C., pure intervals are natural harmonics and therefore simple relations between frequency ratios:
1 : 2 octave (1200 cents)
2 : 3 fifth (701.96 cents)
3 : 4 fourth (498.04 cents)
4 : 5 major third (386.31 cents)
5 : 6 minor third (315.64 cents)
In equal temperament a fifth is 700 cents, a major third 400 cents and a minor third 300 cents. These are compromises most people can adjust their ears to. In Pyhtagorean temperament the fifth is pure, hence 701,96 cents. A major third is 407,84 cents and a minor third 294,12 cents, both even further away from pure than in equal temperament.
Here is a circle of fifths, with cents deviations from equal temperament written next to each note.
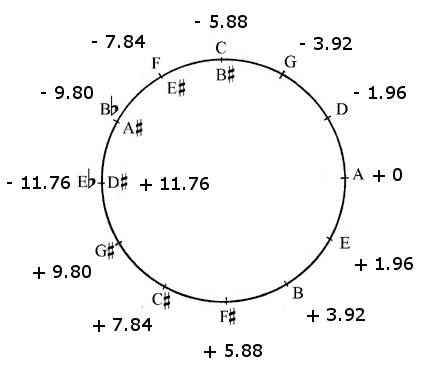
Notice that E-flat is not the same as D-sharp, as it is in equal temperament. You can also not substitute G-sharp with A-flat, etc. And although all other fifths are pure, the fifth between G-sharp and E-flat, or D-sharp and B-flat, depending on which pitch you have chosen to tune the note, is very un-pure: only 678.44 cents. You cannot adjust your ears to this compromise anymore, this fifth is simply too small and very much out of tune. It is called the wolf.
Repositioning of frets
First, take a piece of paper and place it on top of the fingerboard of the lute, one end touching the nut. Now mark the current fret positions on the paper. This way you can put your frets back in their original position later.
Now that we know how many cents higher or lower than equal temperament a note has to be in Pythagorean temperament, we can calculate fret positions. Here is a table with the deviations from equal temperament of each fret, incorporating the deviations from equal temperament of the open courses:
| open string | 1st fret | 2nd fret | 3rd fret | 4th fret | 5th fret | 6th fret | 7th fret | 8th fret |
| G + 3.9 | G# + 13.7 | A + 3.9 | Bb -5.9 | B + 7.8 | C – 2.0 | C# + 11.8 | D + 2.0 | Eb – 7.8 |
| D – 2.0 | Eb – 9.8 | E + 3.9 | F – 5.9 | F# +7.8 | G – 2.0 | G# + 11.8 | A + 2.0 | Bb – 7.8 |
| A + 0 | Bb – 9.8 | B + 3.9 | C – 5.9 | C# + 7.8 | D – 2.0 | Eb – 11.8 | E + 2.0 | F – 7.8 |
| F – 7.8 | F# + 13.7 | G + 3.9 | G# + 17.6 | A + 7.8 | Bb – 2.0 | B + 11.8 | C + 2.0 | C# + 15.7 |
| C – 5.9 | C# + 13.7 | D + 3.9 | Eb – 5.9 | E + 7.8 | F – 2.0 | F# + 11.8 | G + 2.0 | G# + 15.7 |
| G + 3.9 | G# + 13.7 | A + 3.9 | Bb -5.9 | B + 7.8 | C – 2.0 | C# + 11.8 | D + 2.0 | Eb – 7.8 |
This results in the following list of numbers, with which you will have to multiply the string length of your lute to get the new fret positions:
| b | c | d | e | f | g | h | i |
| 0.051 0.064 |
0.111 | 0.156 | 0.210 | 0.250 | 0.288 0.298 |
0.333 | 0.367 0.376 |
For a lute with a string length of 59 cm this would result in the following fret positions in cm:
| b | c | d | e | f | g | h | i |
| 3.0 3.6 |
14.7 | 9.2 | 12.4 | 14.8 | 17.0 17.6 |
19.7 | 21.7 22.2 |
You can mark these fret positions on a similar piece of paper again.
For fret b (first), g (sixth) and i (eighth) we come up with two fret positions: one for notes that are lower than in equal temperament and one for notes that are higher than in equal temperament. On the first fret the lower notes are the e-flat and b-flat on the second and third courses. The higher notes on the first fret are the g-sharp on courses one and six, the f-sharp on the fourth course and the c-sharp on the fifth course. If you want to use notes from both these two groups in one piece, you have to find a solution. One solution is to put the fret in the high position and to glue a little extra fret (called tastini, Italian for ‘little fret’) in the lower position for only the second and third courses. You can use a small bit of fret or matchstick and some tape. A friend of mine uses little custom made ebony wedges. Another solution might be to use two frets.
The g– and i-frets (six and eighth) cause usually no problems, you can place them in either the low or the high position, depending on the piece you play. Just try and listen.
Tuning
Now you only have the fret positions for Pythagorean temperament. Next you will have to tune the open courses of the lute, too. Notice that you do not need a tuner at all, nor, actually, the explanation above to move your frets, as tuning in pure fifths can safely be done by ear alone:
* 1. Tune the third course, a, on a tuning fork.
* 2. Tune the second course, d, by tuning a pure fourth with the third course. You can use the harmonic above the fifth fret of the third course and the seventh fret of the second course.
* 3. Tune the first course, g, by tuning a pure fourth with the second course. You can use the harmonic above the fifth fret of the second course and the seventh fret of the first course.
* 4. Tune the sixth course, g, by tuning a pure double octave with the first course.
* 5. Check the position of the second fret by comparing a (second fret) on the first course with the open third course, and the on the second course (second fret) with the pure fifth on a (or double octave with the harmonic on the seventh fret of the third course).
* 6. Tune the fifth course, c, by tuning a pure fourth with the open sixth course. You can use harmonics again.
* 7. Tune the fourth course, f, by tuning a pure fourth with the open sixth course. You can use harmonics again. Check the octave on the second fret, g, with the open first course.
* 8. Check third fret with f and c on second and third courses with open fourth and fifth courses.
* 9. Check fourth fret by comparing a on fourth course (fourth fret) with the open third course.
* 10. Adjust first fret to either flats or sharps (or add tastini). Flats: octaves e-flat and b-flat on second and third courses with third fret on fifth and first/sixth courses. Sharps: octave f-sharp on second course (fourth fret) with first fret on fourth course.
* 11. Check pure fifths and octaves all over the fingerboard in the positions and keys that you will use. Adjust here necessary and avoid where no solution can be found (e.g. g-sharp on fourth course, third fret).
Back to equal temperament
To put your frets back into their equal temperament positions, you can either use the piece of paper on which you marked them, or calculate their exact positions by multiplying the string length of your lute with the following numbers:
| b | c | d | e | f | g | h | i |
| 0.056 | 0.109 | 0.159 | 0.206 | 0.251 | 0.293 | 0.333 | 0.370 |
Again, for a lute with a string length of 59 cm this will result in the following fret positions in cm:
| b | c | d | e | f | g | h | i |
| 3.3 | 6.4 | 9.4 | 12.2 | 14.8 | 17.3 | 19.6 | 21.8 |
Do not forget to tune the open strings back as well.
More on temperaments for lute in Mean-tone temperament for lute.
David van Ooijen 6/2008